

킬러 문항 삭제 추진 후 첫 9월 모의고사가 출제되었습니다. 국어는 비문학 난이도 하향 조절로 문학은 어려워지고 수학은 수능 시험 시행 이례 가장 쉬웠을 정도로 난이도가 하향되었습니다. 수능 시험은 과거부터 지금까지 계속 변화해 왔습니다. 이번 9월 수학이 쉬웠다고 하여 방심하지 마시고 끝까지 최선을 다해서 공부하셔야 수능날 후회하지 않습니다. 앞으로 남은 시간 두 달, 이젠 익숙한 기출이 아닌 사설 모의고사를 푸셔서 급격히 변화해가는 수학 시험에 적응하셔야 할 때입니다. 오늘은 이지북스 수능리허설 2024학년도 수학 모의평가 사설모의고사 문제집을 리뷰해보고 이번 9월 모의고사와 견주어 비교해보겠습니다.
| 사설 모의고사 이지북스 수능리허설 수학 구성
2024학년도 대학수학능력시험대비 수능리허설 FINAL 모의고사 수학영역은 총 4회분으로 구성되어 있습니다. 해설지, OMR까지 같이 동봉되어 있고, 시험지 질감이나 크기가 실제 수능 시험지와 닮아 있어 실전 연습을 하기 좋습니다.


뿐만 아니라 수1, 수2, 미적-확통-기하 모두 있어서 어느 선택 과목을 선택한 학생이든 풀어보기 좋습니다. 수1, 수2 문제 비율 역시 실제 평가원과 동일할 정도로 디테일한 구성으로 만들어졌습니다.
| 사설 모이고사 이지북스 수능리허설 난이도
난이도는 확실히 이번 9월 모의평가나 작년 수능보단 어렵다고 볼 수 있습니다. 하지만 어려움이 억지스러움이나 불가능할 정도의 가정이나 감각의 영역이 아닌 이미 기출에서 학습한 논리에서부터 기인한 것이기 때문에 풀어볼 가치가 매우 높습니다.

예로, 위 사진의 30번 미분가능 문항은 기존 기출 학습의 집합체입니다. 미분계수를 시컨트 제곱 함수와 다항함수의 곱으로 표현하여 (나)조건에서 특수한 부분적분을 통해 K값을 구하게 하였고, (가)조건에선 부정적분의 상수를 결정지을 수 있게 미분계수값을 주었습니다.
g(x)의 경우 치환 적분을 하도록 만들었습니다. 이처럼 수능리허설의 29, 30번 문제는 어려운 문항이 맞지만 모두 당연히 할 줄 알아야하는 개념을 바탕으로 문제를 만들어 사고력과 순발력을 높일 수 있게 만들었습니다.
수능날 여러분은 100% 집에서 편히 모의고사 풀던 컨디션으로 풀 수 없습니다. 그렇기 때문에 다소 난이도가 있더라도 좋은 문제들로 훈련해야 수능날 어떤 상황이 발생해도 문제를 풀 수 있게 됩니다.
| 문제 퀄리티
9월 모의평가와 수능리허설 문항들을 나란히 두고 비교해보며 말씀드리겠습니다. 왼쪽 문항은 9월 모의평가 문제를 오른쪽 문항에는 수능리허설 문제를 두도록 하겠습니다.

두 문항 모두 범위가 주어진 삼각함수에 관한 것입니다. 평가원은 정말 쉽게 출제하였지만 수능리허설은 각 경우를 구하게 만들어 시간을 좀더 뺏기게 출제하였습니다.
킬러문제 삭제로 준킬러 문항 난이도를 높이려고 하기 때문에 이런 계산이 조금더 들어가는 문항에 대한 면역이 생길수록 더 좋습니다.

기존 평가원 14번은 난이도가 높은 문항의 자리였는데 이번 9평에선 비교적 쉬운 문항으로 출제되었습니다. 지수 함수에 미지수를 첨가하여 조건을 보고 미지수를 확정 짓는 문항입니다.
수능리허설 역시 조건만 기하적인 요소로 바뀌었을 뿐 지수함수의 미지수를 확정 짓는 방향으로 출제되었습니다. 수능리허설 문항들은 묻는 디테일이나 방식이 조금더 논리적이어서 공부하기 좋은 문항들로 구성되어 있습니다.
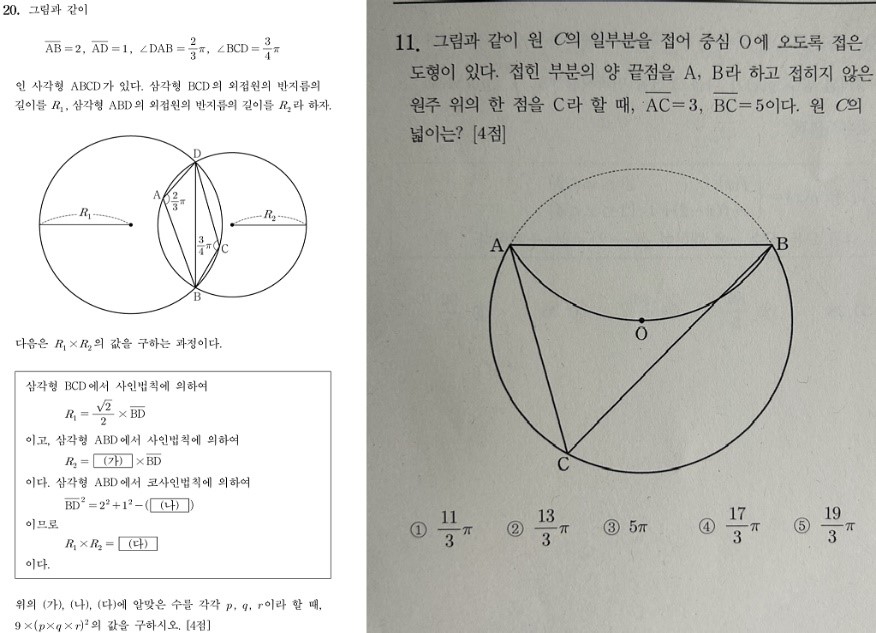
9평 20번 문항은 사인법칙을 활용하여 한 각과 마주보는 변의 길이를 추정하게 만들었습니다.
오른쪽 문항 역시 원을 4분에 1만큼 접어 원의 반지름 조건을 이용하면 각 AOB가 120도 이고 각ACB가 원주각 조건에 의해 60도임을 알 수 있습니다. 평가원은 단순 계산만 시켰지만 수능리허설 사설모의고사는 당연히 알아야할 조건들을 넣어 문제를 풀게 만들었습니다.
이렇게 매해 수능마다 당연히 쓰였던 아이디어들이 들어있는 질 좋은 문제들을 풀 수 있다는 것만으로도 수능 직전에 공부를 효율적으로 하는 것이라고 여겨집니다.

수능 전 마지막 점검이 필요하다면?
수능은 학생들을 서열화해야 하기 때문에 이번 수능 수학 만점이 폭발적으로 많아진 것을 보고 굉장히 어렵게 출제할 가능성이 있습니다. 따라서 수능리허설과 같이 고난도 고퀄리티 문항들로 연습하실 필요가 있습니다.

두 문항 모두 절댓값 함수를 통해 함수가 y=0에서 접힐 때의 미분계수가 0이 되게끔 하는 상수를 결정지으란 문제입니다.
평가원은 단순한 사인 함수로 문항을 냈지만 수능리허설 사설모의고사는 지수함수와 다항함수를 결합하여 출제했습니다. 계산이나 아이디어적으로 수능리허설이 어렵지만 수능에 나올 가능성이 다분한 개념으로 출제하였습니다.

극한의 상황에서 수열값을 묻는 문제입니다. 9월 모평이 좀 더 경우의 수를 나누게 출제되었지만 9평은 29번이었고 수능리허설은 3점짜리 25번입니다. 이처럼 수능리허설은 상당히 평가원을 닮아 있습니다.

이번 수능 30번 문항은 삼각함수 도형의 극한으로 출제되었습니다. 원과 삼각형을 통해 함수를 구해야하는 문항입니다. 수능리허설 28번이 압도적으로 어렵게 출제되었지만 과거 삼각함수 극한 문제를 생각한다면 수능리허설 문항도 적절한 난이도입니다.
| 총평
수능리허설은 평가원을 닮아 있습니다. 풀어볼 가치가 높은 문제들로 구성되어 있어서 이번 수능을 대비하기 좋습니다.
얼마 남지 않은 시간 효율적인 공부를 도와줄 사설 모의고사 수능리허설 추천합니다. 여러분의 수능을 응원합니다! 서포터즈 규동이었습니다.




 경희대학교 의예과
경희대학교 의예과
