

 경희대학교 의예과
경희대학교 의예과

안녕하세요, 이지수능교육 서포터즈로 활동하고 있는 경희대 의예과 22학번 동규입니다. 먼저 6월 모의고사 응시하신다고 고생 많으셨습니다. 작년 6, 9, 수능 난이도와 크게 차이가 나는 문항들은 아니었습니다. 하지만 다양한 유형의 문제를 경험해 보지 못하신 학생분들께서는 푸시면서 겉보기에 굉장히 겁을 많이 먹을 만한 표현과 문제 조건이 있었던 것 같습니다.
성급하게 답을 적고 넘기셨다면 틀릴 만한 문항들도 꽤 있었습니다. 이번 6월 모의고사에서 실수 없이 모두 푸셨다면 수능 때에도 마찬가지로 좋은 결과 있을 것이라고 생각이 됩니다. 다만, 실수를 했거나 잘 모르겠는 유형이 있었다면 반드시 외울 정도로 반복해서 푸시고 직접 조건을 따져가면서 분석해 보시길 바랍니다. 6평과 수능은 연계가 분명히 됩니다.
저는 작년 수능장에서, 6월 모의고사와 수능이 연계가 되었다는 느낌을 받으며 문제를 풀어갔고, 익숙한 형태에 긴장이 낮아져 더 빠르고 정확하게 답을 내고 넘길 수 있었던 경우가 많았습니다. 작년 6월 모의고사 22번 문제에서 3차 함수 그래프 개형 추론을 하는 문항이었고 이 역시 극점을 이용하면 바로 풀리는 문항이었고 작년 수능 22번도 역시 3차 함수 개형 추론이었고, 극점의 위치를 6평 때처럼 의도적으로 찾으려고 노력하여 빠르게 풀 수 있었습니다.
따라서 6평에서 사용했던 아이디어만큼은 외울 정도로 보고 수능장에 들어가야 한다고 생각합니다. 그래서 오늘은 6평 수학을 어떻게 활용하면 좋을지 말씀드리겠습니다. 우선 중요 문항에 대해 말씀드리고, 그리고 남은 9평, 수능을 어떻게 맞이할지 말씀드리겠습니다.
6평에서 볼 문제들 중 공통 문항에 대해서만 언급하겠습니다. 8번, 10번, 12번, 15번, 20번, 21번, 22번 문항입니다.

8번 문항의 경우엔 어렵지 않은 문제이지만, 사실은 평균값 정리에 근거하여서 출제된 문항입니다. x=1, x=5 사이에서 평균 기울기 식을 작성하고 이것이 5 이상이라고 부등식을 작성하면 한 줄 수식으로 답을 낼 수 있습니다. 기본 개념으로 출제한 3점짜리이지만, 개념을 한 번이라도 수능 전 다시 읽어 보시길 추천합니다. 늘 푸시는 그래프 추론 문제만 풀다가 약간만 다른 문제가 쉽게 출제되어도 풀지 못하는 경우는 너무 문제만 풀었기 때문입니다. 다시 한 번 알더라도 개념을 읽어보시면 도움이 될 것입니다. 모든 문제는 개념에 근거하여서 출제되기 때문에, 문제를 보고서 어떤 개념이 쓰였는지 생각하고 그 개념을 의도적으로 사용하면 문제가 아주 간결하게 풀릴 것입니다.
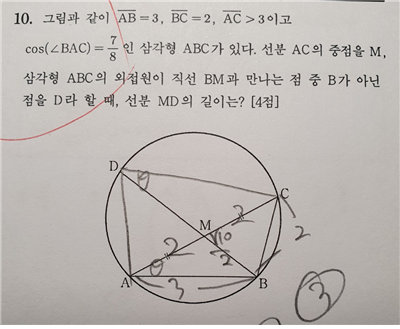
다음으론 10번입니다. 도형에 약한 학생들에게는 어려웠을 수도 있다고 생각됩니다.
문제 논리 순서는 다음과 같습니다. 1) 코사인 법칙을 통해 선분AC의 길이를 구한다. 2) AM=AC=BC=2 임을 알아낸다. 3) 삼각형AMB에서 코사인 법칙을 이용해 MB를 구한다. 4) 닮음을 이용해 길이 닮음식을 작성하여 (MB X MD = AM X AC)을 통해 MD를 구한다. 이렇게 4개의 논리 순서로 답을 낼 수 있습니다. 하지만 여기서 문제인 건 4번째 닮음식인데요. 중학 3학년 도형 파트를 공부한 학생이라면 어렵지 않게 답이 나왔겠지만, 그렇지 않은 학생은 닮음이란 걸 눈치 채지 못하고 답을 못 냈을 겁니다. 따라서 이 아이디어는 반드시 알아두시고, 추가로 원주각, 원의 내접하는 사각형의 성질까지 익히셨으면 좋겠습니다. 그 이상 알아야 할 것이 수능 도형에선 없습니다.
12번 문항은 작년 9평에도 나왔던 형태입니다. 공차가 양수인데 a5와 a7의 곱이 음수이므로 a5는ㄴ 음수, a7은 양수임을 알 수 있습니다. 따라서 a7항 이후는 모두 양수, a5항 이전은 모두 음수이죠. 나)조건을 해석할 때, 좌변의 시그마 항들은 모두 양수여서 절댓값이 사라지는데, 우변의 경우엔 a6항이 음수인지 양수인지 알 수가 없습니다. 이렇게 상황이 한가지로 좁혀지지 않을 때 해야 될 것은 바로 ‘가정’입니다. a6이 양수일 때, a6이 음수일 때 바로 해보시고 모순이 없는 케이스로 답을 내시면 됩니다. 1~2등급 학생들은 케이스가 좁혀지지 않으면 한 치의 고민 없이 바로 케이스를 나누어 문제를 푸는데요, 그 이하의 학생들은 보통 어떻게 하지 고민을 한다고 시간을 버립니다. 따라서 이 문항을 통해 배울 점은 ‘앞으로 케이스가 좁혀지지 않으면 바로 가정하도록 하자’라고 마음을 먹는 것입니다. 이런 태도 교정을 통해 수능날 1등급을 넘어 100점을 받을 수 있습니다.
15번은 작년 9평처럼 수열이 고난도로 나왔습니다. 2015 교육과정에서 수열은 나열을 통해 규칙을 알아보는 것입니다. 처음 보는 수열을 일반화하거나, 규칙을 바로 파악하여 일반항을 작성하라는 것이 아닙니다. 나열을 통한 관찰. 즉, 노가다를 해보라는 것입니다. 항을 나열하다보면 규칙이 보일 것입니다. 4, 6, 8, 10...항들에서 항이 0이 될 수 있는 가능성이 있습니다. 즉 22번 째 항도 0이 될 수 있는 것이죠. 이것은 22번 항까지 전부 나열해보지 않아도 짝수 번째 항에서 보이는 일관된 형태를 통해 알 수 있습니다. 그리고 처음 나열을 하며 케이스를 나눌 때 k=1, 3일 때 a22가 0이 될 수 있음을 알 수 있었습니다. 이처럼 수열을 보고 미리 겁먹지 마시고 그저 나열을 통해 규칙을 알아보십쇼.
20번 문항의 경우는 ‘부정적분으로 표현된 함수‘입니다. 이 유형을 배울 때, 양변을 미분하라고 모든 수험생이 배웠을 겁니다. 이 개념을 떠올리고 의도적으로 미분해서 조건을 대입해보면 ㅣf(2)ㅣ=ㅣf(1)ㅣ ㅣf(5)ㅣ=ㅣf(4)ㅣ임을 알 수 있고 곧장 이차함수에 대입만 해줘도 답이 바로 나옵니다. 작년 6, 9, 수능 모두 20번은 간단히 나왔기에 혹여나 사설 모의고사 20번이 어렵다고 수능날 20번을 건너 뛰지 않으셨으면 좋겠습니다. 수능 역시 그리 어렵지 않게 나올 것입니다.

21번 문항은 아주 자주 나오던 유형입니다. 주어진 로그식=정수k로 두시고 로그의 진수를 2의 지수 꼴인 1/8, 1/64, 1/512라고 해주시면 답이 바로 나오는 유형입니다. 이와 유사한 문항들과 100퍼센트 같은 논리로 출제되었고 앞으로도 그럴 것이니 논리를 익혀두시면 좋을 것 같습니다.
22번 문항은 의외였습니다. 늘 3참 함수 그래프 추론 문항이 나오던 문제 번호였는데 이번 6평은 극한이 나왔습니다. 대입을 통해 어렵지 않게 답이 나올 수 있었습니다. 극한값이 존재하지 않는 t가 두 개이니 그 이상이 나오면 안 됩니다. 이에 착안하여서 식을 조작해주고, 마지막으로 x=0에서 연속이다 한 번만 써주면 답이 나옵니다. 22번을 통해 준비할 점은 수능에 22번에 뭐가 나와도 이상하지 않다는 것입니다. 따라서 앞으로 공부에 있어 거르거나 버리지 마시고 철저히 전부 공부하셔야 될 듯 합니다.
6평을 통해 그동안 공부가 빛을 본 학생도 있겠지만, 그렇지 못한 학생도 있겠죠. 시험 결과가 좋지 않다면 공부법, 그리고 문제풀이 순서가 잘 못 된 가능성이 큽니다. 공부법은 제가 위에 적은 듯이, 개념을 의도적으로 사용하는 방법으로 수학을 풀며 공부하시면 됩니다.
이지수능교육에서 출판 수학 문제집을 이용하면 개념을 적용하는 방식을 체화시키기 좋을 겁니다. 문제풀이 순서는 쉬운 문항을 전부 푸시고서 어려운 문항을 풀되, 문제가 10분이 넘어가도 풀리지 않으면 즉시 버려야 합니다. 이번 모의고사를 통해 본인만의 문제 풀이 순서와 취약점을 배우셨으면 좋겠습니다. 남은 기말고사 잘 치루시고, 9평, 수능까지 힘내시길 바라겠습니다. 이상으로 잉코 서포터즈 동규였습니다.


